Traslacion, rotacion y reflexion de figuras geométricas

ROTACION: Se dice de un cuerpo que esta en rotación cuando todos sus puntos giran alrededor de un mismo eje con la misma velocidad angular. 
Para rotar una figura, se une un vértice de la figura con el centro de rotación mediante un segmento, se traza desde el segmento del ángulo indicado para la rotación y se mide la misma longitud que tiene el segmento anterior marcando el punto imagen.
Se hace lo mismo con cada vértice de la figura y se unen todos los puntos resultantes
La figura que se obtiene es la imagen ´por rotación de la figura original.
El centro de rotación puede estar dentro o fuera de la figura.

 

 

TRASLACION: Un cuerpo se traslada cuando todos sus puntos se mueven paralelamente y con la misma velocidad sin girar, sin cambiar el tamaño, ni ninguna otra cosa solo mover.

 

 

Cada punto de la figura se mueve:

• La misma distancia
• La misma dirección

REFLEXION: Una reflexión es considerada un volteo con respecto a una línea, en una reflexión un objeto geométrico se mueve de un tirón a través de una recta. La recta a través de la cual se refleja un objeto se llama la recta de reflexión o el eje de reflexión.

 

Características de las reflexiones:

 -Un objeto y su reflexión son simétricos sobre la recta de reflexión.

 -Un objeto y su reflexión son congruentes y similares.  

 

 

HOMOTECIAS:

Se conoce homotecia de centro O y razón k (distinto de cero) como la transformación que hace corresponder a un punto A otro A´, alineado con A y O, tal que: OA´=k·OA. Si k>0 se llama homotecia directa y si k<0 se llama homotecia inversa.

Es el cambio de tamaño que se presenta en una figura sin cambiar los ángulos.

 





Análisis de una variable cualitativa

Una variable es cualitativa cuando los valores por los que se toma la variable son cualidades, categorías, o nombres, por ejemplo el sexo del sujeto (Hombre, Mujer).

Al tener las variables cualitativas generalmente se suele realizar un recuento de la cantidad de casos que tenemos de cada categoría posible (frecuencias absolutas) o bien un tanto por ciento el cual contiene las categorías dentro del conjunto de categorías posibles (frecuencias relativas) donde se suele hacer un diagrama de frecuencias o un diagrama de pastel para graficar dichos valores obtenidos.

En ocasiones las variables cuantitativas se categorizan convirtiéndose en cualitativa.

Por ejemplo: Digamos que elegimos los siguientes grupos de edad: menores de 10 años, entre 10 y 20 años y mayores de 20 años, creando tres categorías por medio de una sola variable cuantitativa como lo es la edad.

El caracterizar una variable significa especificar su comportamiento en una población dependiendo de los parámetros establecidos y el tipo de variable ya que se utilizan diversas técnicas ya sea el tipo de variable cualitativa o cuantitativa.

El caso de una variable cualitativa se es necesario poner en orden unos criterios que permitan estudiar o examinar el comportamiento en la población.

Caracterización de dos variables cualitativas

A la hora de llevar a cabo la realización de estudios referentes a una población se es necesario  comparar dos variables cualitativas donde los valores de las variables no son numéricos sino categóricos. Su estructura posterior análisis es lo que nos permite la obtención de conclusiones a partir de la muestra escogida. Se debe utilizar las tablas de contingencia, las tablas marginales y los diagramas de barras para la caracterización de dos variables cualitativas.

Tablas marginales:

En estas tablas se muestran las frecuencias relativas con relación total de cada fila o columna.

Tablas de contingencia:

En una tabla cruzada de contingencia contiene información en cada una de las casillas se le atribuye a la cantidad de sujetos que tienen ambas características, siendo esta una tabla de frecuencias; las filas corresponden a los tipos o clases de una variable cualitativa y las columnas corresponden a las clases de la otra variable cualitativa aplicadas a un entorno definido.

Esta tabla muestra una total distribución de la información obtenida ya que permite tener diversos tipos por lo que se pueden establecer para cada variable de estudio.

En esta tabla de contingencia se observa que:

a. Hay dos variables: Color de ojos y color de cabello.

b. Para la variable “color de ojos” hay 6 tipos de color: Café, verde, azul, ámbar, avellana y miel verdoso.

c. Para la variable “color de cabello” hay 4 variables: Castaño, negro, rubio y rojo.

Diagrama de barras para dos variables:

La representación gráfica de una tabla de contingencia corresponde a un diagrama de barras en el cual se relacionan las clases de las dos variables. Para la tabla anterior e diagrama correspondiente es:

Caracterización de dos variables cuantitativas: 

Ejemplo: En busca del mejoramiento del nivel de nutrición de los niños de un jardín infantil, se está realizando un proyecto, el cual cosiste en comprobar la cantidad de frutas que estos consumen en la semana, para llevar a cabo este proyecto, se desarrolló una encuesta entre 24 familias las cuales tienen a sus hijos en el jardín. Las respuestas obtenidas por la encuesta se dieron en unidades de fruta y los resultados fueron los siguientes:

3 2 4 3 0 1 2 2 1 2 5 0

1 3 0 4 2 2 1 3 1 0 2 3

La variable Unidades de fruta es cuantitativa

Al igual que las variables cualitativas, las variables cuantitativas necesitan de una caracterización para poder fijar las conclusiones sobre ellas, por lo que su caracterización se debe realizar teniendo en cuenta la manera en la que se van a presentar los datos.

Para esto, se tienen en cuenta dos pautas:

a. Si los datos están agrupados: Cuando los datos obtenidos a partir de una variable cualitativa se van a presentar en forma agrupada se utilizan las siguientes herramientas para su caracterización.

b. Si los datos no están agrupados.

Diagrama de tallo y hojas:

En esta representación gráfica se dividen o clasifican los datos de acuerdo con la expresión decimal de cada uno. El tallo corresponde a la primera o primeras cifras del dato y en la mayoría de los casos la hoja corresponde a la última cifra del dato.

Tablas de distribución de frecuencia:

Una tabla de distribución de frecuencias para variables cuantitativas está formada por intervalos de clase (donde se clasifica cada uno de los datos, los intervalos deben ser disjuntos y ordenados, esto quiere decir que un dato sólo puede ser clasificado en un intervalo y estos deben abarcar desde el dato más pequeño hasta el más grande y está determinado por un límite inferior y un límite superior), frecuencia del Intervalo “f” (es el número de individuos o datos que se clasifican en cada intervalo), frecuencia relativa “fr” (medida que relaciona por medio de un cociente la frecuencia de cada intervalo con el total  de individuos o datos  recogidos), frecuencia Acumulada “F” (sumatoria del número de individuos que están en los intervalos anteriores  y la frecuencia del intervalo), frecuencia relativa acumulada “Fr” (corresponde a la relación y por medio de un cociente entre la frecuencia acumulada de cada intervalo y total de datos.) y marca de clase “M_i” (Es el punto medio de los límites de cada intervalo, se utiliza para graficar las distribuciones de frecuencias. La marca de clases es el dato representativo de cada intervalo)

Ejemplo:

Elaboremos una tabla de frecuencias para los datos que se encuentran en la siguiente tabla

Tabla 1:

El número de intervalos a utilizar es 8 por lo que:

√64 – 8

Tamaño del intervalo:

((37.9-32.1)/8) - 5.8/8 – 0.725 ≈ 0.7

Conclusiones a partir de la tabla:

a.       El 8% de las camisas fue fabricado con un material que contenía entre el 32.1% y el 32.8% de algodón y un porcentaje igual fue fabricado con un material que contenía entre el 36.9% y el 38.4% de algodón.

b.      El 84% de las camisas fue fabricado con un material que contenía entre el 32.9% y el 36.8% de algodón

Polígono de Frecuencias:

Es un diagrama formado al asignar a cada marca de clase la frecuencia correspondiente a cada intervalo.

Circunferencia

La circunferencia es una línea curva y plana o bien el lugar geométrico donde los puntos de un plano se encuentran a igual distancia del centro en una cantidad constante mejor conocida como radio. La circunferencia debe distinguirse del círculo el cual es el lugar geométrico que contiene los puntos en dicha circunferencia, donde están a una distancia igual al radio y los demás puntos a menor distancia que el radio o también la circunferencia es el perímetro del círculo.

La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad.

Propiedades:

En la circunferencia, existen diversos puntos, rectas y segmentos que son:

El Centro: Punto interior equidistante de cada uno de los puntos de una circunferencia.

El Radio: El radio es igual a la longitud de la circunferencia dividida entre 2π. Es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma y mide la mitad del diámetro.

El Diámetro: El diámetro de una circunferencia mide el doble del radio y es el segmento que une dos puntos de la circunferencia el cual pasa por el centro. El diámetro es igual a la longitud de la circunferencia dividida entre π.

Cuerda: Segmento que une dos puntos de la circunferencia donde el diámetro es la cuerda de longitud máxima.

El Arco: El arco de la circunferencia es cada una de las partes en que una cuerda divide a la circunferencia y se denota con el símbolo sobre las letras de los puntos extremos del arco.

Semicircunferencia: Cada uno de los dos arcos iguales delimitados por los extremos de un diámetro. Es la mitad de una circunferencia.

        

Longitud de la semicircunferencia: 

Posiciones relativas de una recta y una circunferencia en el plano:

Recta secante: Línea que corta a la circunferencia en dos puntos.

Recta tangente: Es la línea que toca a la circunferencia en un sólo punto.

Punto de Tangencia: Punto o lugar de contacto de la recta tangente con la circunferencia.

Recta exterior: No tiene ningún punto de corte con la circunferencia.

Posiciones relativas de dos circunferencias en el plano:

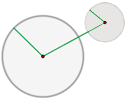
Exteriores:

La distancia entre los centros es mayor que la suma de las radios. Las circunferencias no tienen puntos en común.

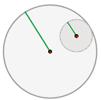
Interiores:

La distancia entre los centros es menor que la diferencia de los radios y es mayor que cero; una circunferencia está dentro de otra por lo que no tienen ningún punto en común.

Concéntricas:

Los centros coinciden. No tienen puntos en común, salvo que R=R1, en este caso son la misma circunferencia.

Tangentes exteriores:

La distancia entre los centros es igual a la suma de los radios. El centro de cada circunferencia es exterior a la otra y tienen un punto en común, punto de tangencia.

Tangentes interiores:

La distancia entre los centros es igual a la diferencia entre los radios. El centro de una de las circunferencias está dentro de la otra. Tienen un punto en común.

Cuando tienen dos puntos en común:

Interior:

Su distancia al centro es menor que el radio.

Punto sobre la circunferencia:

Su distancia al centro es igual que el radio.

Punto exterior a la circunferencia:

Su distancia al centro es mayor que el radio.

Secantes:

La distancia entre los centros es mayor que la diferencia de los radios.

Ecuación canónica de la circunferencia

(x – h)² + (y – k)² = r² Donde las coordenadas del centro son (h, k) y “r” el radio de la circunferencia. Ejemplo: Determinar la ecuación de la circunferencia que pasa por el punto (6,3) y cuyo centro se encuentra en C(0,0)

Ecuación general de la circunferencia

Si conocemos el centro y el radio de una circunferencia, podemos construir su ecuación ordinaria y si operamos los cuadrados, obtenemos la forma general de la ecuación de la circunferencia, así:      X² + Y² + Dx + Ey + F = 0

Prueba:

Ejemplo:

1. Hallar la ecuación general de la circunferencia con centro C(2;6) y radio r = 4

(x - 2)² + (y - 6)² = 4²

X² - 2(2x) + 2² + y² - 2(6y) + 6² = 4²

X² - 4x + 4 + y² - 12y + 36 = 16

X² + y² - 4x - 12y + 4 + 36 - 16 =0

X² + y² - 4x - 12y + 24 = 0

D = -4      E = -12      F = 24

2. Deducir la ecuación general de la circunferencia a partir de la ecuación canónica

“(x – h)² + (y – k)² = r²”

 Determinar la ecuación general de la circunferencia con centro en (- 1, 1) y cuyo radio mide

unidades

                                

(X - (- 1))² + (Y - 1)² = ()²

(X + 1)² + (Y - 1)² = 3

X² + 2X + 1 + Y² - 2Y - 1 = 0

X² + Y² + 2X - 2Y - 1 = 0  -------------- Ecuación general de la circunferencia.

Cónicas

La cónica es una curva que se obtiene a partir de cortar o intersectar una superficie cónica por un plano. Las cónicas propiamente dichas se obtienen cuando no pasan por el vértice del plano; como en el caso de un cono circular recto de dos hojas cuyo plano no pasa por su vértice. Según el ángulo y el lugar de intersección se dividen en cuatro tipos que son eclipse, parábola, circunferencia e hipérbola.

Por lo que si el plano únicamente toca uno de los mantos del cono sin ser paralelo a una de sus aristas como resultado se obtendrá una Eclipse. Si el plano intersecta los dos mantos de dicho cono, se obtendrá una Hipérbola. Finalmente si el plano que corta es paralelo a una de las aristas, a partir del cono se obtendrá una parábola.

Las cuatro secciones cónicas en el plano:

Superficie cónica de revolución

Es la superficie engendrada por una recta denominada generatriz que gira alrededor de otra fija llamada eje, a la que intersecta en un punto que se llama vértice o ápice, por lo que el ángulo bajo el que la generatriz corta al eje es constante y la superficie cónica delimita al volumen denominado cono.

Es importante recordar que partiendo de una circunferencia (e=0) se aumenta la excentricidad obteniendo eclipses, parábolas e hipérbolas.

Aplicaciones

Aerodinámica: Son de importancia en su aplicación industrial, porque permiten repetirse a través de medios mecánicos con gran exactitud, logrando superficies, formas y curvas perfectas.

Morfología (diseño)

Gravitación

Geometría proyectiva.

FUNCIONES TRIGONOMETRICAS

Las funciones trigonométricas tienen como objetivo principal la medición de triángulos

Las definiciones de las funciones trigonométricas son:

• SENO: Es la razón entre el cateto opuesto al ángulo y la hipotenusa.
• COSENO: Es la razón entre el cateto adyacente al ángulo y la hipotenusa.
• TANGENTE: Es la razón entre el cateto opuesto al ángulo y el cateto adyacente al ángulo.
• COTANGENTE: Es la razón entre el cateto adyacente al ángulo y el cateto opuesto al ángulo.
• SECANTE: Es la razón entre la hipotenusa y el cateto adyacente al ángulo.
• COSECANTE: Es la razón entre la hipotenusa y el cateto opuesto al ángulo.

EJEMPLO

 

También se pueden resolver triángulos por medio de la ley de senos y la ley de cosenos, pero estos solo aplican para triángulos no rectángulos

• LEY DE SENOS:  relación entre los lados y ángulos de triángulos no rectángulos (oblicuos). Simplemente, establece que la relación de la longitud de un lado de un triángulo al seno del ángulo opuesto a ese lado es igual para todos los lados y ángulos en un triángulo dado

 

• LEY DE COSENOS:  usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la ley de los senos porque no podemos establecer una proporción que pueda resolverse

       c² = a² + b² – 2abcos C.

    b² = a² + c² – 2accos B

     a² = b² + c² – 2bccos A



 

CIRCUNFERENCIA UNITARIA

Estamos hablando de aquella circunferencia donde su origen y su radio es la unidad

 

En la figura, el punto P(x,y) representa las coordenadas de punto "P" que pertenece a la circunferencia unitaria.

En el triángulo rectángulo se tiene que:

X² +Y²=1

Por lo tanto los puntos P(x,y) que pertenecen a la circunferencia unitaria cumplen con la ecuación de la circunferencia.

 

https://www.youtube.com/watch?v=JYtAE77QgEM, Éste video nos proporciona una información mas compleja sobre el tema, como construirlo y para que sirve

TEOREMA DE PITÁGORAS

Cuando tenemos un triangulo rectángulo el cuadrado de la hipotenusa equivale a la suma de los cuadrados de los otros dos lados

 

 

En base a lo dicho anteriormente podemos deducir que la suma c elevado al cuadrado y b elevado al cuadrado es igual a a elevado al cuadrado asi:

 

 

EJEMPLO:

 

 

En este triángulo podemos observar que la hipotenusa es igual a 5 y los otros dos catetos equivalen respectivamente a 3 y 4, entonces

 

3² + 4² = 5²

 

9 + 16 = 25

 

      25 = 25

 

 

Este teorema nos resulta muy útil cuando necesitamos hallar un lado de el triángulo y nos dan solo 2 de sus lados.